Attenuator Theory of Operation
To start with, let’s evaluate basic characteristics of a passive attenuator. As the name suggests, this component produces an output signal that is lower in power than its input. Most attenuators that you buy off the shelf come with fixed attenuation at levels such as 3 dB, 6 dB, 10 dB, 20 dB, or even more. Mathematically, we can describe attenuation with a simple equation, shown below.
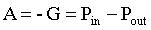
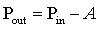
Equations 1 and 2. Relationship between power and attenuation.
All terms in both equations are expressed in terms of dB. Based on equations 1 and 2, it is clear that if we have a signal at -40 dBm, a 20 dB attenuator will reduce the power level to -60 dBm.
In order to understand the use and limitations of external attenuators in practical applications, it is important to discuss the RF attenuation available on today’s signal generators. To start with, let’s first evaluate where attenuation might be present on a superheterodyne vector signal generator, illustrated in the figure below:
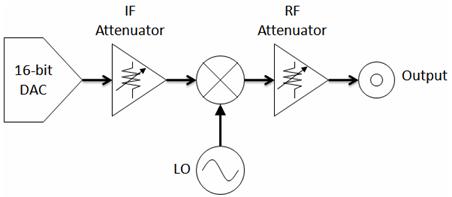
Figure 1. Diagram of a superheterodyne vector signal generator.
While the diagram in figure1 is over-simplified (we’ve stripped filters, amplifiers, etc.), we can see that attenuation is applied at either the IF or RF stage. In this diagram, a digital to analog converter (DAC) (in this case 16-bit) is used to generate an IF signal. Note that a small signal loss will also occur at the mixer, but we will assume the mixer loss is 0 dB for the sake of argument in this paper. On the whole, programmable IF and RF attenuation are the most prominent ways to reduce signal power.
For example, suppose you wanted to generate CW tone at 1 GHz at a power level of -60 dBm. In this scenario, an IF signal is generated with a 16-bit DAC at a voltage level of approximately 1 Vptp. In order to understand the level of attenuation that must be applied to attenuate this signal to -60 dBm, let’s first understand how 1 Vptp might translate to a power level in dBm with the following:
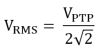
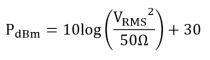
Equations 3 and 4. RMS voltage and Power as a function of peak-to-peak
Using the equations above, we determine that a 1 Vptp signal has a power level of approximately +4 dBm.
Thus, assuming there is zero path loss in the RF signal chain, the generator must apply 64 dB of attenuation to produce the desired power level of -60 dBm.
Highly sensitive receivers, however, often require a test stimulus with power levels well below the maximum attenuation IF or RF attenuation available on the instrument. In this scenario, digital attenuation must also be applied before the DAC to reduce the IF power. By applying digital attenuation, the full-scale range (and also full dynamic range) of the DAC is no longer used due to bit quantization. However, the “unused” part of the dynamic range is the portion that would have been otherwise buried in the noise floor of the instrument. In fact, external attenuation is required to extend dynamic range below the noise floor of the instrument.
We can prove this theoretically by first examining the relationship between dynamic range and bit resolution of a typical DAC. Generally, a DAC produces 6.02 dB of dynamic range for each bit of resolution. More specifically, we can represent the dynamic range as a function of the number of bits, ‘n’, in the following equation:
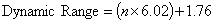
Equation 5. Dynamic range as a function of number of bits
Thus, a 16-bit DAC will have a theoretical dynamic range of ((16 x 6.02) + 1.76) = 98.08 dB. Of course, the theoretical value is based purely on bit quantization and does not account for non-linear signal products which cause spurs, harmonics, and other types of distortion. For the sake of argument, lets assume that our distortion products are 10 dB, resulting in a usable dynamic range, SFDR (spurious-free dynamic range), of 88 dB (98 – 10 dB).
Based on our calculation of dynamic range for a 16-bit DAC, it is easy to see why digital IF attenuation is often used at lower power levels. As an example, suppose you wanted to generate a signal at -120 dBm. If an instrument produces an average noise density of -160 dBm/Hz, only 40 dB of SFDR is required to generate this signal. Thus, if our DAC has 88 dB of SFDR, up to 48 dB (88 - 40 dB) of digital gain can be applied without affecting the SFDR of the resulting test stimulus. This can be visualized in the image below:
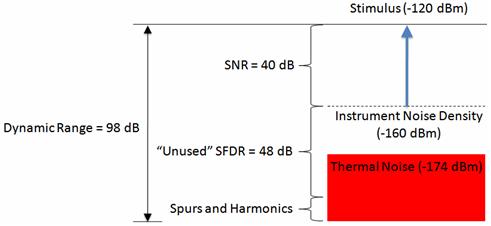
Figure 2. Dynamic range lost due to instrument noise density
In the scenario where a DAC produces an output at +4 dBm, 124 dB of total attenuation is needed to produce an output at -120 dBm. The PXIe-5672 vector signal generator addresses this requirement by applying 87 dB of IF/RF attenuation and 37 dB of digital attenuation, resulting in a total attenuation of 124 dB.
Based on the system described above, a combination of IF and RF attenuation can be applied by the instrument to lower the RF power level without introducing noise. However, in some scenarios, adding additional attenuation with an external attenuator can provide added advantages. The main two advantages, described in the subsequent sections, include improvements in amplitude accuracy and the extension of dynamic range at low power levels.
Improving Amplitude Accuracy
While many factors affect amplitude accuracy, one of the biggest sources of amplitude error is VSWR, or voltage standing ratio. In a perfect world, the impedance of both an RF instrument (typically 50 ohms) and the DUT (device under test) are matched. However, even slight impedance mismatches produce VSWR, which cause the incident signal to be reflected back to the source. Reflections can have a substantial affect on the test stimulus. In fact, depending on the phase difference between the stimulus and reflection, these products can either increase or decrease the amplitude of the composite RF signal. Typically VSWR is determined by measuring reflection coefficient of the materials being used. This is noted in the equation below, where ‘ρ’ is the reflection coefficient:
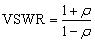
Equation 6. VSWR as a function of the reflection coefficient
Based on the VSWR of the transmission line, we can then calculate the return loss (RL) or amplitude of the reflection. Return loss is determined by the following equation:
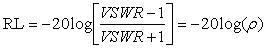
Equation 7. Return loss as a function of VSWR
Note that while the amplitude of reflections are certainly predictable, the phase is not. Because the reflection’s phase determines whether it will increase or decrease overall power, VSWR results in amplitude inaccuracy.
Fortunately, the effects of VSWR can be reduced substantially by using an external attenuator. This is particularly helpful at lower power levels, where attenuation must already be used. When using an attenuator, we can think of reflections of actually being attenuated twice. This is illustrated in the figure below:
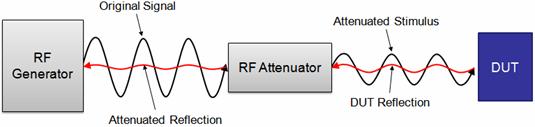
Figure 3. Attenuator improves power accuracy by attenuating reflection
As figure 3 illustrates, the external attenuator attenuates the reflection caused by the DUT. As a result, the affect of VSWR will be minimized and amplitude accuracy will be improved.
Dynamic Range Extension
A second motivation for using external attenuators to test low-sensitivity receivers is to reduce the noise density of the test signal. In this scenario, the attenuator reduces both noise power and signal power. As purely passive RF device, attenuators theoretically inject no noise into an RF signal. For example, suppose we generate a 1 GHz tone at 0 dBm with a SNR of 80 dB. In this scenario, the average noise density of the signal should be exactly -80 dBm/Hz. If a 20 dB passive attenuator is applied to the signal, the SNR will theoretically remain constant. Thus, the output of the attenuator will is -20 dBm and a noise power will is -100 dBm. Thus, attenuators can be particularly helpful at power levels that are close to the average noise density of the RF instrument. In this scenario, they can actually be used to extend our dynamic range by lowering the noise floor of the test stimulus.
For example, supposed we wanted to generate a signal with a SNR of 50 dB at a power level of -120 dBm. Without attenuation, an example instrument (such as the PXIe-5672) will have an average noise density of -158 dBm/Hz. Thus, our instrument can only provide us with 38 dB (-120 + 158) of dynamic range at this power level. As a result an attenuator is required to attenuate the noise to the desired level of -170 dBm to produce an SNR of 50 dB. In this scenario, the instrument is configured to have a power level of -100 dBm, and a 20 dB attenuator is used to attenuate the signal by 20 dB to -120 dBm. Moreover, our noise level is attenuated to the theoretical minimum of -174 dBm. Thus, our dynamic range has increased from 38 dB to 54 dB, which is the theoretical maximum dynamic range at the desired power level. To illustrate this concept, we graphically represent the output power of a signal generator with and without attenuation.
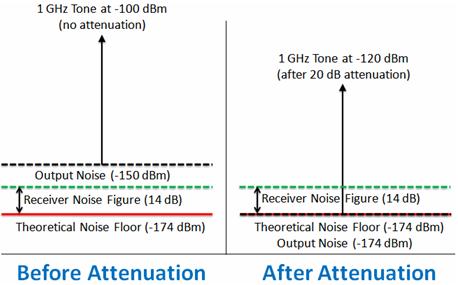
Figure 4. Noise level before and after attenuation
As the figure above illustrates, an attenuator can be used to reduce both the output power and the output noise of a signal generator. Note, however, that it is not able to attenuate a signal below the theoretical noise floor (thermal noise) at: -174 dBm/Hz.
Realistically, receiver sensitivity test will only require you to supply a noise figure that is only slightly below the noise figure of the receiver. Thus, if the receiver has a noise figure of 14 dB, we should ensure that our test stimulus has an output noise density that is less than -160 dBm/Hz. While the noise density of a generator can be reduced to -174 dBm/Hz, this will have diminishing benefits for test accuracy, since the noise introduced by receiver components will mask noise introduced by the generator.
As an example, we can use a PXI-5661 vector signal analyzer along with a PXI-5690 Pre-Amp to operate as a low-noise receiver. Combined with the preamp, our VSA will should have a typical average noise density of -165 dBm/Hz. This is equivalent to a high sensitivity receiver with a 9 dB noise figure.
First, we will use the PXI-5671 vector signal generate to generate a CW tone at 1 GHz. At this power level the typical output noise density of the generator is specified at -158 dBm/Hz. When the test stimulus is displayed in the vector signal analyzer, in 1 Hz bandwidth, we can observe that the displayed average noise floor is -157 dBm/Hz, shown below:
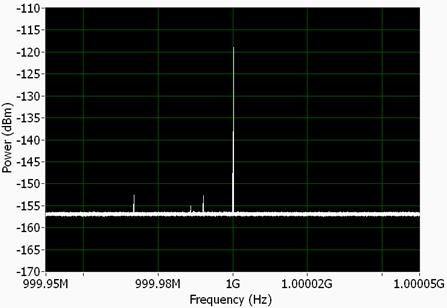
Figure 5. Noise floor at -157 dBm/Hz without attenuation
As figure 5 illustrates, we are only using roughly 40 dB of the DAC’s dynamic range, since digital attenuation is being used. To extend the dynamic range of our instrument, we simply add an external attenuator to our instrument. With a 20 dB attenuator, our noise level should be reduced to the thermal noise level of -174 dBm/Hz. Note that the noise level, in this case, is attenuated by less than 20 dB, because it cannot be attenuated below the thermal noise level. When applying attenuation, we must also adjust the output level to compensate for power lost. Since our desired output power is -120 dBm, we configure the vector signal generator to have an output power of -100 dBm when using a 20 dB attenuator.
When viewing an attenuated output with our vector signal generator, the displayed average noise level (DANL) should be dominated by the noise figure of the analyzer, and not the generator. With our PXI-5661/PXI-5690 VSA/Pre-amp combination, the typical noise floor is -165 dBm/Hz. Our actual measurement is illustrated in the figure below:
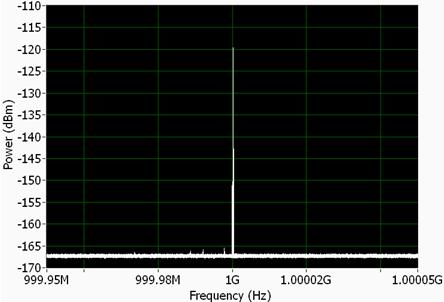
Figure 6. Noise floor at -167 dBm/Hz without attenuation.
With attenuation added to the test stimulus, we can observe a noise density is -167 dBm/Hz. As stated above, the noise density is dominated by the analyzer. However, we can clearly see that the generator is outputting a signal with a noise level that is at least lower than -167 dBm/Hz.
While the example above seems fairly straightforward, it is important to clarify that noise can never be attenuated to lower than -174 dBm/Hz at room temperature. In other words, while an attenuator is able to attenuate active noise that has been introduced by a component, it is NOT able to attenuate thermal noise at the theoretical noise floor.
The scenario above is often a source of confusion for RF engineers, because it is commonly known that the noise figure of any passive component is equal to its loss. Noise figure (NF) and noise factor (F), are commonly described in terms of the ratio of input SNR to output SNR at the specific temperature of 290 K. As described in the equations below, noise figure is simply the logarithmic equivalent of the noise factor measurement.
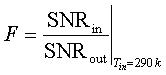
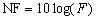
Equations 8 and 9. Relationship between SNR and noise figure (NF)
Based on the equations above, it might seem that the use of an attenuator on the output of a vector signal generator would attenuate the signal strength without attenuating the noise power. However, it is important to recognize the equation for noise figure ONLY relevant when the noise level is equal to the thermal noise density at -174 dBm/Hz. In general, terms such as noise figure and noise factor should only be applied to wireless receivers, since the noise power from an antenna at 290K will be approximately -174 dBm/Hz.
For example, suppose a receiver observes a signal with a SNR of 60 dB at a power level of -114 dBm. In this scenario, applying a 20 dB attenuator would attenuate the signal power by 20 dB to -134 dBm. However, the noise level would remain unchanged, since the noise power is already at the thermal noise level. Thus, when Pnoise = -174 dBm/Hz, the noise figure of a passive attenuator is equivalent to its loss.
On the other hand, output noise density from an RF generator is caused by active components and will result at levels that are sometimes significantly above the theoretical noise floor. In this scenario, noise power can be attenuated to the level of the thermal noise floor. As a result, high sensitivity receivers can be tested with a stimulus which has a noise power that is well below that of the signal generator.