Calculating Line-to-Line Voltages from Line-to-Neutral Measurements with the NI 9225 C Series Voltage Input Module

Assume you have a Y-connected 240 Vac three-phase system as shown below in figure 1. The NI 9225 C Series Voltage Input Module is connected between each phase and neutral:

Figure 1. 240V 3-Phase System connected to NI 9225 300V AI module
 

Each channel in the NI 9225 will nominally have 240 Vrms between the AI+ and AI- terminal. The NI 9225 is rated to 300 Vrms from channel to earth, so the measurement is within the safety specifications. Assuming a perfectly balanced system, each phase is separated by 120 degrees and the line-to-neutral voltage on each phase is the same. As long as these two assumptions hold true, then the magnitude of the line to line voltage is 1.732 * Vp , where Vp is the line-to-neutral voltage. If the line-to-neutral voltage is 240Vrms, then the line-to-line voltage will be 416 Vrms. The NI 9225 is rated for 600 V ch-ch isolation, so this voltage is within the safety specifications. 
 

The connection scheme shown above in figure 1 can be used to indirectly measure the line-to-line voltages on a Y-connected systems. The line-to-line voltage is the vector sum of the line to neutral voltages. So, for example, if we know V_an, V_bn, and V_cn (defined as in the diagram below), we can find the line to line voltages as follows:
 

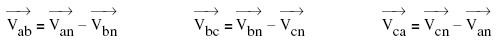
The following phasor diagram (diagram 1) will help visualize the phasor math required to convert from line-to-neutral voltages to line-to-line voltages.

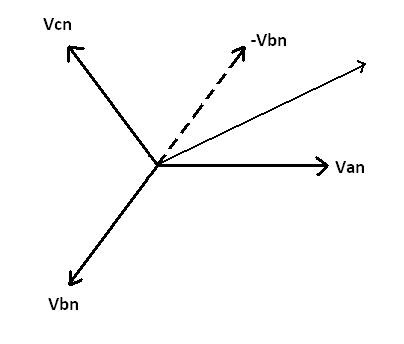
Diagram 1. Line-to-line calculation phasors
 

We will start with an example showing how to measure V_ab.  As has been described above, the line-to-line voltage is the phasor sum of the line-to-neutral voltages, so
 

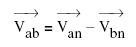
Nominally, each phase in a three phase system is spaced exactly 120 degrees apart. However, since our intent is to perform measurements in the system, we cannot assume it to be ideal. Because of this, instead of assuming 120 degrees of separation between phases, we will simply use Θ_xx to denote the angle between two phases. V_an as defined above has zero phase, and V_bn has a phase of Θ_ab.
 

Breaking up V_bn into rectangular components results in the following:
 

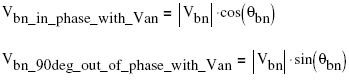
Subtracting the in-phase component of V_bn from V_an:

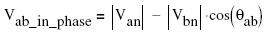
From the rectangular components, we can calculate the magnitude of the line to line voltage:

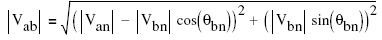
To calculate the phase angle Θ_ab, we now find the phase of the rectangular vector calculated above:

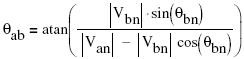
To illustrate the above, we assume the line-to-neutral voltages are 240 V, and the phase to phase angle is 240 V.
 

V_ab = 415.7V (as referenced in the first paragraph of this document)

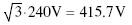
Θ_ab = 30

IMPORTANT: The assumption that the line-to-line voltage is sqrt(3) times the line-to-neutral voltage is only valid when the magnitudes of the line-to-neutral voltages are all the same.
 

If we can guarantee that the line-to-line phase is exactly 120 degrees, then the equations above can be somewhat simplified. This may be the case when the power source is a generator with three rotor windings physically 120 degrees apart. If we again look at the example of finding V_ab based on V_an and V_bn, the magnitude and phase can be calculated as follows:

This eliminates the need to calculate sine and cosine functions, although the square root and arctangent operations are still needed.
 

The NI 9225 can be used to measure line-to-neutral voltages, which can in turn be used to calculate line to line parameters. However, it must be noted that the relationship between line-to-neutral and line-to-line voltages involves magnitude and phase, and both must be taken into account in order to obtain accurate line-to-line measurements. The phasor diagram below (diagram 2) shows the magnitude and phase relationship between all line-to-neutral and line-to-line voltages in the system.

Diagram 2. Magnitude and phase relationship of all voltages in system