Unexpected or Inconsistent Numeric Comparison Logic in LabVIEW

Issue Details

• I am comparing floating-point numeric values in LabVIEW. Sometimes the logic executes as expected and other times it does not. 
• I am measuring data until a certain value is measured. However, sometimes the comparison function does not recognize that both values (value measured and stop value defined in code) are equal. I am having trouble understanding why the issue occurs, and even more why it only happens sometimes.

Solution

This is a known problem in numerical mathematics. Therefore it is expected in all programming languages. As most floating point numbers do not have an exact representation in binary, comparing them for equality can yield unexpected results.


Floating-point numbers are represented internally as a binary approximation, causing calculations that would be exact in decimal notation to often not be exact in binary as small rounding errors occur in outer decimal places of the values. For example, a computer can and will often compare 0.1 + 0.2 = 0.3 as false, as the binary representation of the equation's both sides could execute to a value only close to the exact value like e.g. 0.3000000000044 (or any number of similar rounded-off variants depending on the machine and compilation order), rendering the equality false.


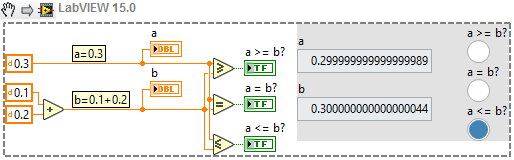
To avoid this, when using comparison logic with floating-point values, use one of the following methods:

• Compare for "greater or equal" or "less or equal" instead for "equal".
• Compare while allowing an absolute difference (absolute epsilon).
• Compare to within relative epsilon.
• Compare to within a given digit of precision by converting the numbers to strings.
• Compare using integers.